Lista de Exercícios

1) No jogo da jarra d'água, temos 2 jarras, uma com capacidade para 3 litros (A) e outra com capacidade para 4 litros (B). Inicialmente, A e B estão vazias. Podemos encher cada jarra com água de uma torneira T, podemos esvaziar qualquer jarra jogando a água fora, ou pasando água de uma jarra para outra. Queremos encontrar um conjunto de operações que deixe exatamente 2 litros de água na jarra B. (Uma solução complicada: encher A com água da torneira, despejar conteúdo de A em B, encher A novamente na torneira, despejar conteúdo de A em B até B encher, jogar fora água de B, despejar conteúdo de A em B.)

a) Formular o espaço de busca deste problema:

• Descrever o estado inicial (utilizar algu a estrutura de dados para representar o estaod inicial)
• Apresentar a condição que testa se os estados são estado final
• Defina os operadores e apresente descrições precisas (algorítmicas) da função de cada operador.

b) Desenhe um grafo contendo todos os nós distintos do espaço de busca até o nível três e mostre o caminho da solução.

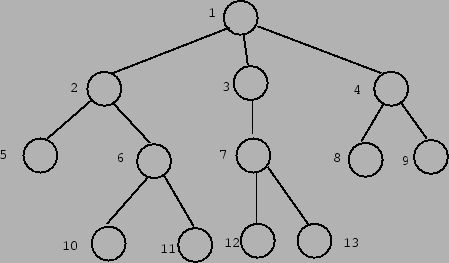
2) Apresente a ordem de visita dos nós da árvore da figura 1 para cada uma das estratégias abaixo (escolha nós mais à esquerda na árvore em todos os casos):

a) Busca em profundidade

b) Busca em profundidade iterativa (aumentando o nível de 1 a cada iteração

c) Busca em largura

Figure 1: Grafo para exercício 2

3) Considere uma árvore finita de profundidade d e fator de ramificação b. (uma árvore com apenas o nó raiz tem profundidade zero; uma árvore contendo apenas a raiz e seus b sucessores tem nível 1 e assim por diante). Suponha que o nó objetivo mais raso da árvore tenha profundidade $g \leq d$.

a) Qual é o número máximo e mínimo de nós gerados segundo busca em profundidade limitada no nível d?

b) Qual é o número máximo e mínimo de nós gerados segundo busca em largura?

4) Assuma que conseguimos gerar 100.000 nós por segundo em uma busca em largura. Assuma que gastamos 100 bytes para armazenar cada nó. Qual é a quantidade de memória total gasta e tempo de execução com profundidade d e fator de ramificação 5. Mostre o crescimento para cada nível numa tabela.

5) Assuma que estamos percorrendo uma árvore com fator de ramificação b. Porém devido a estados repetidos, não temos a certeza de estarmos gerando uma árvore (por causa dos ciclos). Se testarmos estados repetidos (contra todos já gerados até o estado corrente) quantas verificações deverão ser feitas em nível d?

6) Baseando-se no grafo da figura 2, mostre como as seguintes estratégias de busca chegariam do nó S ao nó G:

(a) busca limitada em profundidade com limite 3.

(b) busca iterativa em profundidade.

(c) busca de custo uniforme.

(d) bidirecional com busca em profundidade do estado inicial para o final e busca em largura do estado final para o inicial.

(e) ``hill-climbing''.

(f) busca best-first.

(g) A*.

(h) SMA* com limite de 3 nós.

Figure 2: Grafo para exercício 1

Todas as estratégias encontram a solução? Alguma encontra a solução ótima? (indique qual é a solução ótima).

7) Prove que o algoritmo A* é admissível.

8) Considere a árvore da figura 3.

Figure 3: Árvore para exercício 3

Explore a árvore utilizando o algoritmo ALFA-BETA. Indique todas as partes da árvore que serão cortadas. Indique o caminho (ou os caminhos) para o vencedor e remova da árvore todos os valores (função utilidade) que não necessitam ser computados.

9) Escreva um procedimento em pseudo-código para busca ``best-first'' e busca em largura (não omita detalhes relevantes para o entendimento do algoritmo). Aplique seus algoritmos ao problema do jogo dos oito (justifique e defina os movimentos possíveis), mostrando a árvore de busca até o nível 3. Utilize as seguintes configurações inicial e final:

               4 7 1      1 2 3
               8 3 2  =>  4 5 6
               5   6      7 8

10) Execute o algoritmo alfa-beta (da esquerda para a direita) na árvore da figura 4.

Figure 4: Árvore para exercício 5